Треугольник - это геометрическая фигура, которая вызывает интерес и изучается как профессиональными математиками, так и учениками начальной школы. Одной из самых популярных задач, связанных с треугольником, является решение задачи о делении его высоты пополам. Эта задача требует знания основных математических понятий и навыков решения простых уравнений.
Деление высоты треугольника на равные части имеет свои практические применения: например, она может быть использована для определения координат центра тяжести треугольника или для расчета площади треугольника, если известна его высота.
Решение данной задачи может быть представлено в виде системы уравнений или геометрической конструкции. В обоих случаях требуется знание основных свойств треугольника и умение работать с простыми математическими операциями.
Задача о делении высоты треугольника напополам
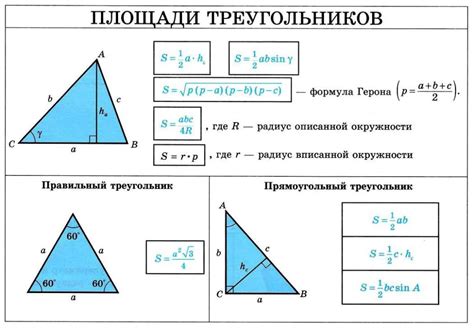
Задача о делении высоты треугольника напополам основывается на свойствах высот треугольника и их отношениях. Цель задачи состоит в том, чтобы найти точку на высоте треугольника, которая делит ее на две равные части.
Для решения этой задачи можно использовать такую же методику, как и для решения задачи о делении медианы. Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Медиана также делит высоту напополам.
Метод решения задачи о делении высоты треугольника напополам заключается в построении медианы к стороне, противоположной данной высоте. Далее, найдя середину этой медианы, мы найдем точку, которая делит заданную высоту напополам.
Для решения задачи об делении высоты треугольника напополам можно использовать следующий алгоритм:
- Построить треугольник по заданным сторонам.
- Построить высоту треугольника, проходящую через одну из его вершин.
- Найти середину стороны, противоположной заданной вершине.
- Соединить найденную середину со вершиной треугольника, через которую проходит высота.
- Точка пересечения построенной медианы с заданной высотой будет делить ее напополам.
Решение этой задачи может быть полезным при решении других задач, связанных с применением свойств треугольников и их высот. Также, знание методики решения данной задачи поможет в изучении геометрии и ее применении в различных областях, включая науку, инженерию и архитектуру.
Треугольник
Треугольники могут быть разных типов в зависимости от своих свойств. Наиболее распространенные типы треугольников - это прямоугольный, равнобедренный и разносторонний треугольники.
Прямоугольный треугольник имеет один прямой угол, который равен 90 градусам. Равнобедренный треугольник имеет две равные стороны и два равных угла. Разносторонний треугольник имеет все три стороны и углы разной величины.
Треугольник можно описать с помощью трех свойств - его стороны, углы и высоту. Стороны треугольника обозначаются буквами a, b и c, а углы - буквами A, B и C.
В треугольнике существует несколько способов деления его высоты пополам. Один из таких способов - это использование теоремы о подобных треугольниках. Согласно этой теореме, высота треугольника делит его основание на две части пропорционально длинам отрезков основания.
Таким образом, деление высоты треугольника пополам позволяет найти длину одной из его частей и использовать ее в дальнейших вычислениях или решении задач.
Определение треугольника
Особенности треугольника включают в себя:
- Сумма всех внутренних углов треугольника равна 180 градусам.
- Угол противоположный самой длинной стороне треугольника является наибольшим углом, а углы противоположные боковым сторонам меньше.
- Треугольник может быть равносторонним (если все его стороны равны), равнобедренным (если две стороны равны), прямоугольным (если один из его углов равен 90 градусам), или общего типа (если ни одно из этих условий не выполняется).
Определение треугольника основано на его свойствах и характеристиках. Изучение этих свойств позволяет решать задачи, связанные с треугольником, включая задачу о делении его высоты пополам.
Свойства треугольника
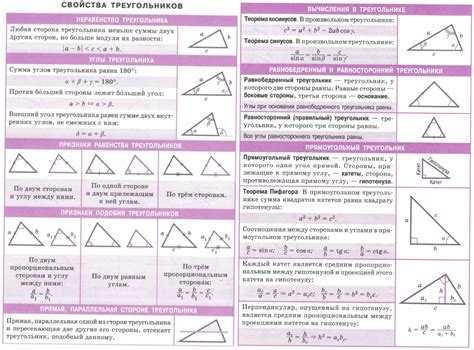
- Треугольник имеет три стороны и три угла.
- Сумма всех углов треугольника равна 180 градусам.
- Наибольшая сторона треугольника называется гипотенузой, а оставшиеся две стороны - катетами.
- Сумма длин любых двух сторон треугольника всегда больше длины третьей стороны.
- Высота треугольника - это перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение.
Деление высоты треугольника пополам - это важное свойство, которое может быть использовано для решения задач, связанных с треугольниками. Например, одно из применений этого свойства - определение центра окружности, описанной около треугольника, который является точкой пересечения трех высот треугольника.
Высота треугольника
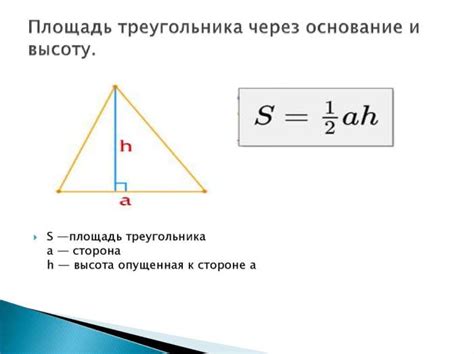
Знание высоты треугольника может быть полезно при решении задач, связанных с вычислением площади треугольника или нахождением его других характеристик, например, описанной окружности или медианы.
Чтобы вычислить высоту треугольника, можно использовать различные методы, в зависимости от известных данных. Например, если известны длины сторон треугольника, то высота может быть найдена с помощью формулы Герона. Если известны координаты вершин треугольника, то высота может быть найдена с помощью формулы для расстояния между точкой и прямой. Также существует известная формула для вычисления высоты на основе площади треугольника и длины стороны.
Высота треугольника играет важную роль в геометрии и имеет множество приложений в различных областях, включая архитектуру, строительство, физику и геодезию.
Важно заметить, что при делении высоты треугольника пополам, получается отрезок, который является высотой для каждой из полученных половин треугольника.
Произвольный треугольник
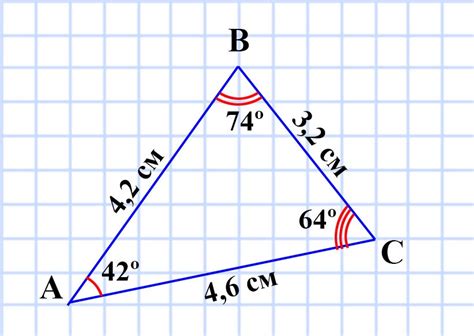
В случае произвольного треугольника, деление его высоты на две равные части может быть более сложной задачей. Однако, с использованием геометрических свойств треугольника, можно найти способ разделить высоту на две равные части.
Для этого можно использовать следующий алгоритм:
- Пусть треугольник задан своими вершинами A, B и C.
- Найдите длины всех сторон треугольника: AB, BC и AC.
- Найдите периметр треугольника, который равен сумме длин всех сторон: P = AB + BC + AC.
- Используйте формулу Герона для вычисления площади треугольника: S = sqrt(P(P-AB)(P-BC)(P-AC)), где sqrt обозначает квадратный корень.
- Вычислите высоту треугольника как отношение удвоенной площади к длине стороны: h = 2S/AB.
- Разделите высоту на две равные части: h/2.
Теперь вы знаете, как разделить высоту произвольного треугольника на две равные части с использованием геометрических формул. Этот метод позволяет найти точку деления высоты на две равные части и решить задачу деления высоты треугольника пополам.
Деление высоты пополам
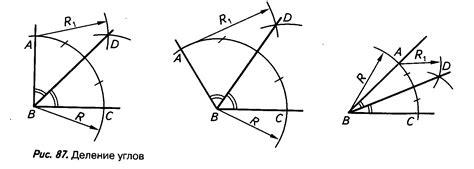
Для решения этой задачи необходимо вначале найти длины сторон треугольника. Затем используя теорему Пифагора, определяется длина высоты треугольника. Далее, используя подобие треугольников, можно найти точку деления высоты пополам.
Решение этой задачи имеет практическое применение в различных областях, включая строительство, архитектуру и картографию. Например, в архитектуре можно использовать деление высоты пополам для определения центра тяжести здания, что позволяет распределять нагрузку равномерно и обеспечивать его устойчивость.
Таким образом, задача о делении высоты пополам является важной в геометрии и имеет широкие практические применения. Решение этой задачи требует применения знаний теорем Пифагора и подобия треугольников.
Задача о делении высоты пополам

Для решения этой задачи можно применить различные методы. Один из самых простых способов – использование свойств подобных треугольников. Для этого можно воспользоваться тем фактом, что высота, проведенная к основанию треугольника, делит его на два подобных треугольника и соответственно, их высоты также подобны.
Пусть треугольник ABC имеет высоту, проведенную из вершины C, и она делит сторону AB на две равные части в точке D. Также пусть точка E – основание этой высоты.
Используя подобные треугольники, можно установить соотношение между отрезками CD и DE:
CD/DE = AC/AE
Так как треугольники ABC и ADE подобны, соотношение становится:
CD/DE = AB/AD
Зная, что CD и DE равны (так как высота делит отрезок AB пополам), можно записать свойство:
CD/CD = AB/AD
Сократив отношение на CD, получаем:
1 = AB/AD
Отсюда следует, что отрезок AD равен отрезку AB. То есть, высота проведена в равнобедренный треугольник, и она делит сторону пополам.
Таким образом, задача о делении высоты пополам может быть решена с использованием свойств подобных треугольников. Это позволяет находить точку, в которой высота делит сторону треугольника пополам, с помощью простых математических операций.



