В математике принадлежность точки графику функции является важным понятием, позволяющим определить, лежит ли данная точка на графике функции или нет. Рассмотрим функцию y = 0,5x, где x - это аргумент функции, а y - ее значение. Если точка (x, y) принадлежит графику этой функции, то она удовлетворяет уравнению y = 0,5x.
Функция y = 0,5x представляет собой прямую линию, проходящую через начало координат и образующую угол с положительным направлением оси OX. Таким образом, все точки этой прямой лежат на графике функции.
Для определения принадлежности точки графику функции y = 0,5x, необходимо подставить координаты данной точки в уравнение функции и проверить его истинность. Если результат равенство верно, то точка принадлежит графику функции, а если нет - то не принадлежит.
Таким образом, для функции y = 0,5x принадлежность точки (x, y) графику можно проверить, подставив ее координаты в уравнение этой функции и убедившись, что результат равенство верен.
Принадлежность графику функции y = 0,5x точки
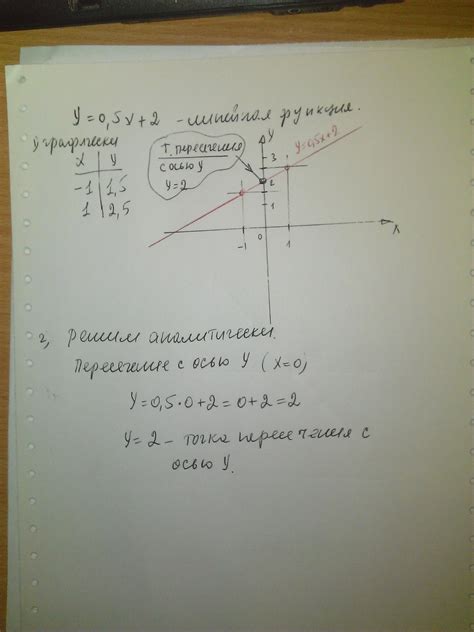
Чтобы определить принадлежность точки графику этой функции, необходимо знать ее координаты. Пусть данная точка имеет координаты (x0, y0).
Если мы подставим эти значения в уравнение функции y = 0,5x, то получим утверждение: y0 = 0,5 * x0.
То есть, если координаты точки удовлетворяют этому равенству, то она принадлежит графику функции y = 0,5x. Если равенство не выполняется, то точка не принадлежит графику функции.
Например, если у нас есть точка (2, 1), для проверки ее принадлежности мы подставим x = 2 и y = 1 в уравнение y = 0,5x:
1 = 0,5 * 2
1 = 1
В данном случае равенство выполнено, поэтому точка (2, 1) принадлежит графику функции y = 0,5x.
Таким образом, принадлежность точки графику функции y = 0,5x определяется подстановкой ее координат в уравнение и проверкой выполнения равенства.
Определение принадлежности

Для определения принадлежности точки к графику функции y = 0,5x, необходимо подставить координаты точки в уравнение функции и проверить результат. Если полученное значение y равно 0,5, то точка принадлежит графику функции, иначе точка не принадлежит.
Например, для точки (2, 1) подставим координаты в уравнение функции:
y = 0,5 * x
1 = 0,5 * 2
1 = 1
Результат равен 1, что не равно 0,5. Значит, точка (2, 1) не принадлежит графику функции y = 0,5x.
Точки, лежащие на графике функции y = 0,5x, образуют прямую линию, проходящую через начало координат (0, 0) и имеющую угловой коэффициент 0,5. Таким образом, все точки на этой прямой принадлежат графику функции.
Критерии определения принадлежности точки графику
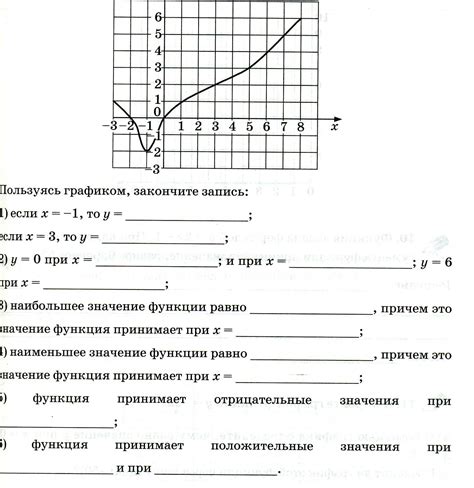
Для определения принадлежности точки графику функции y = 0,5x необходимо провести несколько проверок. Во-первых, можно подставить координаты точки в уравнение функции и убедиться, что равенство выполняется. Если точка лежит на графике, то ее координаты должны удовлетворять уравнению.
Кроме того, можно построить график функции и визуально сравнить его с положением точки. Если точка лежит на графике, то она должна совпадать с одной из точек линии функции.
Еще одним критерием является производная функции. Если точка лежит на графике функции y = 0,5x, то ее координаты должны удовлетворять условию, что производная функции в этой точке равна 0,5. Таким образом, можно вычислить производную функции в заданной точке и проверить выполнение условия.
Важно учитывать, что эти критерии являются необходимыми, но не достаточными условиями принадлежности точки графику функции y = 0,5x. Иногда точка может удовлетворять всем условиям, но не лежать на графике функции. Поэтому рекомендуется проводить все необходимые проверки для определения принадлежности точки графику.
Алгоритм определения принадлежности
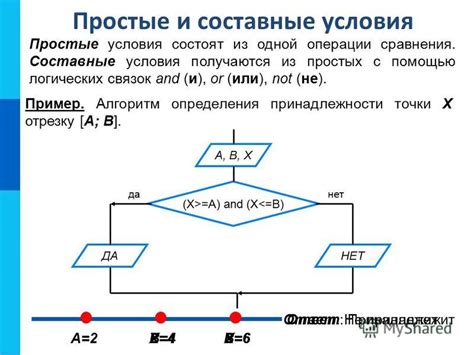
Шаг 1: Получим значения коэффициента наклона и смещения для графика функции y = 0,5x.
Для уравнения y = mx + b, где m - коэффициент наклона и b - смещение, получаем m = 0,5 и b = 0.
Шаг 2: Введите значения координат точки, которую необходимо проверить на принадлежность графику.
Шаг 3: Используя уравнение прямой, подставьте значения координат точки вместо x и y: y = 0,5x + 0.
Шаг 4: Выполните вычисления.
Шаг 5: Если полученная в шаге 4 значение y совпадает с заданным значением y для точки, то точка принадлежит графику функции.
Пример: Для точки (2, 1) проверим ее принадлежность графику функции y = 0,5x.
Шаг 1: m = 0,5, b = 0.
Шаг 2: Координаты точки (2, 1).
Шаг 3: Подставляем значения: 1 = 0,5 * 2 + 0.
Шаг 4: Выполняем вычисление: 1 = 1 + 0.
Шаг 5: Полученное значение (1) совпадает с заданным значением y для точки. Точка (2, 1) принадлежит графику функции y = 0,5x.
Последовательность действий для определения принадлежности точки графику

Для определения принадлежности точки графику функции y = 0,5x, следуйте следующей последовательности действий:
- Запишите уравнение функции y = 0,5x.
- Подставьте координаты точки в уравнение функции.
- Выполните вычисления и запишите результат.
- Сравните полученный результат с координатой y точки.
- Если результат вычисления совпадает с координатой y точки, то точка принадлежит графику функции y = 0,5x. В противном случае, точка не принадлежит графику функции.
Например, пусть дана точка А с координатами (2, 1). Для проверки принадлежности этой точки графику функции y = 0,5x:
1. Уравнение функции: y = 0,5x
2. Подставляем координаты точки А: y = 0,5 * 2 = 1
3. Полученный результат: y = 1
4. Сравниваем полученный результат (y = 1) с координатой y точки А (1).
5. Так как результат совпадает с координатой y точки, точка А принадлежит графику функции y = 0,5x.
Зависимость от углового коэффициента
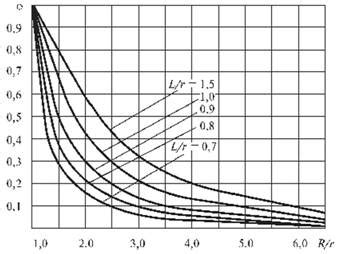
Уравнение графика функции y = 0,5x задает прямую линию с угловым коэффициентом равным 0,5. Угловой коэффициент (также известный как коэффициент наклона) определяет, насколько быстро функция растет или уменьшается при изменении переменной x. В данном случае, коэффициент равен половине, что означает, что функция будет расти вдвое медленнее, чем при угловом коэффициенте равном 1.
Угловой коэффициент также определяет направление функции на графике. Если коэффициент положителен, то график будет наклонен вверх и функция будет увеличиваться при увеличении значения переменной x. Если коэффициент отрицательный, то график будет наклонен вниз и функция будет уменьшаться при увеличении значения переменной x.
В случае уравнения y = 0,5x, график будет наклонен вверх, так как угловой коэффициент положителен. Это означает, что при увеличении значения x, значение y будет увеличиваться. Такой график можно встретить, например, при исследовании зависимости времени пробежки от дистанции, если каждый километр пробегался со средней скоростью 0,5 км/ч.
Важно отметить, что угловой коэффициент определяет только наклон и направление графика, но не его абсолютные значения. Для определения конкретных точек на графике необходимо также знать начальные условия или добавить дополнительные уравнения.
Изменение принадлежности в зависимости от значения углового коэффициента
Если угловой коэффициент отрицательный, то график функции будет убывать - линия будет идти вниз с левого к правому. В этом случае точки, удовлетворяющие уравнению y = 0,5x, будут находиться ниже графика функции.
Если угловой коэффициент равен нулю, то график функции будет горизонтальной линией, и любая точка, удовлетворяющая уравнению y = 0,5x, будет находиться на этой линии.
Таким образом, принадлежность графику функции y = 0,5x определяется угловым коэффициентом и позволяет нам выявить положение точек относительно графика функции.
Примеры определения принадлежности
Определение принадлежности точки графику функции y = 0,5x осуществляется путем подстановки координат точки в уравнение функции и проверки выполнения равенства.
Для примера, рассмотрим точку А с координатами (2,1). Подставляем эти значения в уравнение функции:
y = 0,5 * x
1 = 0,5 * 2
1 = 1
Так как равенство выполняется, точка А принадлежит графику функции y = 0,5x.
Аналогичным образом можно определить принадлежность других точек графику функции. Например, для точки В с координатами (4,-2):
y = 0,5 * x
-2 = 0,5 * 4
-2 = 2
Равенство не выполняется, поэтому точка В не принадлежит графику функции y = 0,5x.
Таким образом, определение принадлежности точек графику функции y = 0,5x основывается на проверке равенства уравнения функции для каждой точки.
Реальные примеры принадлежности точки графику функции y = 0,5x
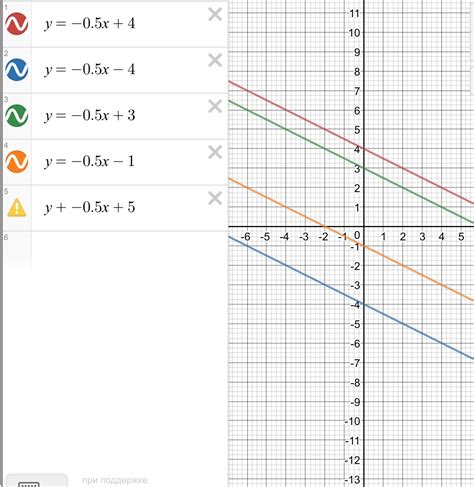
График функции y = 0,5x представляет собой прямую линию, которая проходит через начало координат и имеет положительный наклон. В реальной жизни можно наблюдать множество примеров, где точки лежат на данном графике.
Например, допустим у вас есть задача с постоянной скоростью движения автомобиля. Если график функции y = 0,5x представляет зависимость пройденного пути (y) от времени (x), то точки на этом графике будут соответствовать моментам времени и пройденному расстоянию.
Другой пример - рост растения. Если график функции y = 0,5x отображает зависимость высоты растения (y) от времени (x), то точки на этой прямой будут представлять собой пары значений времени и высоты, соответствующие конкретным моментам роста растения.
Таким образом, график функции y = 0,5x находит свое применение в различных областях - от физики и математики до экономики и биологии, благодаря своей простоте и универсальности. Это позволяет анализировать и предсказывать различные явления, основываясь на данный графике и его точках.



