Движение точки по окружности является одним из фундаментальных понятий в физике и геометрии. Но насколько постоянна скорость точки при таком движении? Давайте рассмотрим этот вопрос более подробно.
Многие люди думают, что скорость точки, движущейся по окружности, является постоянной. Однако это не совсем верно. Если посмотреть внимательно, то можно увидеть, что при движении по окружности точка изменяет свою скорость.
В начале движения точка находится в максимальном удалении от центра окружности и ее скорость является максимальной. По мере приближения к центру, скорость точки уменьшается и достигает минимума в момент, когда она проходит через сам центр. После этого скорость начинает снова увеличиваться по мере удаления от центра.
Основные принципы движения точки по окружности
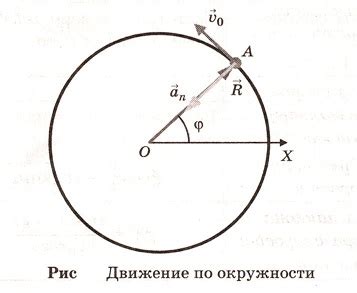
1. Траектория движения точки по окружности всегда является замкнутой кривой, которая образуется в результате постоянного радиуса окружности.
2. Скорость движения точки по окружности постоянно изменяется, но ее величина всегда остается постоянной.
3. Направление скорости точки по окружности всегда перпендикулярно касательной к траектории движения.
4. Ускорение точки по окружности всегда направлено к центру окружности и называется центростремительным ускорением.
Также стоит отметить, что скорость прямо пропорциональна радиусу окружности и обратно пропорциональна периоду движения точки. Это значит, что чем больше радиус окружности или меньше период движения, тем больше скорость точки.
Таким образом, движение точки по окружности представляет собой сложную взаимосвязь между радиусом окружности, периодом движения, скоростью и ускорением. Изучение этих принципов позволяет более глубоко понять и объяснить физический мир и его законы.
Равномерность: характер движения точки

Равномерное движение по окружности характеризуется равномерностью скорости и постоянством направления движения. В данном случае величина скорости остается постоянной, а ее направление всегда совпадает с направлением радиуса к окружности.
Скорость точки, движущейся по окружности, всегда направлена по касательной к окружности в каждой точке пути. Но, несмотря на постоянное направление скорости, величина ее изменяется, так как точка проходит разную длину окружности за разное время.
Таким образом, скорость точки, движущейся по окружности, не постоянна, но она является подвижной величиной с определенной зависимостью от времени. В то же время, можно сказать, что скорость движения точки по окружности является равномерной, так как ее вектор и направление могут изменяться только вдоль касательной.
Таким образом, характер движения точки по окружности является равномерным по скорости, но не равномерным по ускорению. Величина скорости постоянна, а ускорение изменяется.
Скорость точки на окружности: постоянная или изменчивая?

Для того чтобы понять, почему скорость точки на окружности меняется, необходимо вспомнить основные свойства движения по окружности. В частности, радиус окружности определяет путь, который проходит точка за единицу времени. Таким образом, скорость точки на окружности зависит от радиуса окружности и времени, которое она затрачивает на прохождение одного оборота.
Иными словами, при увеличении радиуса окружности скорость точки увеличивается, а при увеличении времени, затрачиваемого на один оборот, скорость точки уменьшается. Таким образом, можно заключить, что скорость точки на окружности является переменной величиной.
Однако стоит отметить, что хотя скорость точки на окружности изменяется, ее направление остается постоянным. Направление скорости всегда перпендикулярно радиусу окружности в точке, где находится точка. Это свойство движения по окружности является следствием радиальной силы, действующей на точку.
Таким образом, можно сказать, что скорость точки на окружности является переменной величиной, которая зависит от радиуса окружности и времени, затрачиваемого на прохождение одного оборота. Направление скорости точки на окружности остается постоянным и всегда перпендикулярно радиусу окружности в точке, где находится точка.
Центростремительная сила и ее влияние на скорость
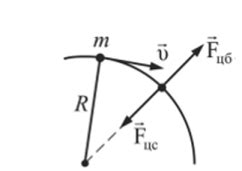
В движении точки по окружности важную роль играет центростремительная сила. Эта сила всегда направлена к центру окружности и вызывает ускорение точки в этом направлении. Рассмотрим, как центростремительная сила влияет на скорость точки.
Когда точка движется по окружности со скоростью V, она постоянно меняет направление своего движения. Это значит, что точка постоянно испытывает ускорение в направлении центра окружности. Чем больше скорость точки, тем больше ускорение она испытывает.
Центростремительная сила, действующая на точку, равна произведению ее массы на квадрат скорости и деленное на радиус окружности:
Fc = m * V^2 / R
Здесь Fc - центростремительная сила, m - масса точки, V - скорость точки, R - радиус окружности.
Из этой формулы видно, что центростремительная сила пропорциональна квадрату скорости точки и обратно пропорциональна радиусу окружности. Если скорость точки увеличивается, то и центростремительная сила увеличивается. Если радиус окружности уменьшается, то и центростремительная сила увеличивается.
Центростремительная сила не влияет на величину скорости точки, но она влияет на ее направление. Отсюда следует, что скорость точки постоянна, но она постоянно меняет направление. Таким образом, при движении точки по окружности ее скорость постоянна, но она не является постоянной векторной величиной. Точка движется равномерно по окружности, но не равномерно по траектории.
Зависимость скорости от радиуса окружности и периода обращения
Скорость точки на окружности зависит от ее радиуса. Чем меньше радиус окружности, тем большую скорость имеет точка, двигаясь по нему. Это связано с тем, что при сравнительно малых радиусах окружности точка проходит меньшее расстояние за то же время, что приводит к увеличению ее скорости.
Кроме того, скорость точки на окружности зависит от периода обращения. Период обращения - это время, за которое точка совершает полный круг по окружности. Чем меньше период обращения, тем больше скорость точки на окружности. Если точка движется быстро и совершает полный оборот за очень короткое время, то ее скорость будет очень высокой.
Таблица ниже показывает зависимость скорости точки от радиуса окружности и периода обращения:
| Радиус окружности | Период обращения | Скорость точки |
|---|---|---|
| Маленький | Долгий | Маленькая |
| Большой | Долгий | Большая |
| Маленький | Короткий | Большая |
| Большой | Короткий | Очень большая |
Таким образом, скорость точки на окружности не является постоянной и зависит от радиуса окружности и периода обращения. Эта зависимость позволяет точке двигаться с различной скоростью по окружности в зависимости от этих параметров.
Применение знаний о скорости точки на окружности в практических задачах
Знание о скорости точки на окружности имеет широкое практическое применение в различных задачах. Вот несколько примеров, где эти знания могут быть полезны:
- Машиностроение: при разработке колесных механизмов, роторов турбин и двигателей, знание о скорости точки на окружности позволяет расчетывать требуемые параметры для оптимальной работы механизмов.
- Астрономия: при изучении движения планет и спутников, знание о скорости точки на окружности позволяет предсказывать их траектории и расчетывать времена прохождения различных точек.
- Авиация: при разработке крыльев самолетов и лопастей вертолетов, знание о скорости точки на окружности помогает определить оптимальную форму и длину лопастей для достижения максимальной подъемной силы.
- Физика: при изучении вращательного движения тел, знание о скорости точки на окружности позволяет определить момент инерции тела и силу, действующую на него.
- Математика: знание о скорости точки на окружности используется при решении геометрических задач, например, при нахождении тангенты к окружности в заданной точке.
Описанные примеры демонстрируют, как важны знания о скорости точки на окружности в практическом применении. Они позволяют решать интересные и сложные задачи в различных областях науки и техники, а также способствуют развитию и совершенствованию этих областей.



