В мире чисел зачастую встречается интересная особенность: разность двух простых чисел может каким-то образом вести себя неожиданно. Такое сравнение простых чисел открывает перед нами дверь в фундаментальные вопросы о структуре числовых последовательностей.
Скажем, простые числа сами по себе являются основой для множества математических размышлений и открытий. Они представляют собой числа, которые делятся без остатка только на себя и на единицу. Простые числа - это такие числа, которые нельзя разложить на множители, кроме как на единицу и само число.
Однако, если мы возьмем два простых числа и вычтем одно из другого, полученная разность может каким-то образом нарушить это правило и стать составным числом. Вопрос заключается в том, всегда ли разность простых чисел будет составным числом? Давайте разберемся.
Влияет ли разность простых чисел на их составность?

Математически говоря, разность двух простых чисел может быть как составным, так и простым числом. Это зависит от значения самих простых чисел и их разности. Если разность простых чисел равна 1, то она будет составным числом, так как делится на 1 и само себя. Но если разность больше 1 и не делится ни на одно другое число, кроме 1 и себя самого, то она будет простым числом.
Примером разности простых чисел, являющейся простым числом, может служить разность между 11 и 7, которая равна 4. Данная разность не делится ни на какое другое число, кроме 1 и 4, значит она является простым числом.
Однако, не всегда разность простых чисел является простым числом. Например, разность между 11 и 5 равна 6, которая делится на числа 1, 2, 3 и 6. Таким образом, данная разность является составным числом.
Определение простых чисел
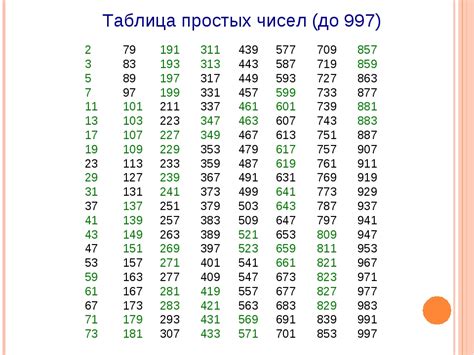
Например, число 2 является простым числом, так как единственные его делители - 1 и 2. А число 4 уже не является простым числом, так как его делители - 1, 2 и 4.
Простые числа имеют множество уникальных свойств и являются важными в математике. Их распределение по числовой оси является одной из центральных тем исследования. Существует множество алгоритмов для проверки числа на простоту и генерации простых чисел.
| Простые числа | Делители |
|---|---|
| 2 | 1, 2 |
| 3 | 1, 3 |
| 5 | 1, 5 |
| 7 | 1, 7 |
| ... | ... |
Таким образом, простые числа играют важную роль в математике и имеют свойства, которые делают их уникальными. Понимание и изучение простых чисел помогает лучше понять структуру числовой оси и математические закономерности.
Примеры простых чисел

Вот некоторые примеры простых чисел:
- 2 - самое маленькое простое число, которое является четным.
- 3 - следующее простое число после 2, также является нечетным.
- 5 - следующее нечетное простое число после 3.
- 7 - простое число, следующее после 5.
- 11 - простое число, которое не делится нацело ни на одно число от 2 до 10.
- 13 - следующее простое число после 11.
- 17 - простое число, следующее после 13.
Простые числа можно найти на протяжении бесконечного ряда, и они играют важную роль в различных областях науки и технологий.
Что такое составное число?

Например, число 4 является составным, так как оно делится не только на 1 и на само себя (4), но также на 2. Также число 12 является составным, так как его можно разделить на 1, 2, 3, 4, 6 и 12. В отличие от составных чисел, простые числа имеют только два делителя – 1 и само число.
Существует бесконечное количество составных чисел, в отличие от простых чисел, которые меньше бесконечности. Ключевой момент при определении составного числа заключается в наличии делителей, отличных от 1 и самого числа.
Знание о составных числах имеет большое значение в математике, включая области криптографии и факторизации больших чисел, так как несоставные числа служат основой для построения простых чисел и других математических структур.
Может ли разность простых чисел быть составным числом?

Однако, если разность двух простых чисел является составным числом, то это означает, что она имеет более двух делителей. Это может произойти, когда разность чисел делится на другое число без остатка. Например, разность чисел 7 и 3 равна 4, которая является составным числом, так как она делится на 2 без остатка.
Таким образом, разность простых чисел может быть как простым, так и составным числом в зависимости от выбранных чисел. Из этого следует, что нет однозначного ответа на вопрос о том, всегда ли разность простых чисел является составным числом.
Доказательство того, что разность простых чисел не всегда является составным числом

Первые шаги в исследовании этого вопроса были сделаны уже в античности. Многие греческие математики, такие как Евклид, Аристотель и Пифагор, изучали свойства и особенности простых чисел. Они наблюдали, что разность простых чисел может быть как составным, так и простым числом. Они сформулировали некоторые гипотезы, которые помогли в дальнейших исследованиях, но окончательного доказательства не получилось.
С течением времени, математики не прекращали искать доказательства или противопримеры для утверждения о том, что разность простых чисел всегда является составным числом. Однако, несмотря на все усилия, такого доказательства до сих пор нет.
В истории математики были найдены множество примеров, когда разность простых чисел может быть как составным, так и простым числом. Некоторые из них удивляют и вызывают интерес. Например, число 2 и 3 - это простые числа, а разность 3 - 2 = 1 - это составное число. В то же время, числа 5 и 2 - тоже простые числа, а разность 5 - 2 = 3 - это простое число.
Итак, можно сказать, что вопрос о том, всегда ли разность простых чисел является составным числом, до сих пор остается открытым. Математики продолжают исследовать этот вопрос и надеяться на то, что рано или поздно удастся найти доказательство для этого явления.



